Pitágoras de Samos (siglo VI a.C.) es conocido principalmente por su célebre teorema matemático, pero su impacto va mucho más allá de las matemáticas. Para muchos, fue el primero en descubrir la relación entre los números y la música, lo que lo convierte en una figura clave en la historia de la música. Su estudio de las proporciones musicales no solo transformó la música en una ciencia, sino que también sentó las bases para profundas reflexiones filosóficas y geométricas que influyeron en el pensamiento occidental.
Pitágoras y el descubrimiento de las proporciones musicales
La leyenda cuenta que Pitágoras descubrió las relaciones entre los sonidos musicales y los números mientras pasaba frente a una herrería y escuchó cómo los martillos producían diferentes tonos al golpear el metal. Intrigado, realizó una serie de experimentos con cuerdas, campanas y flautas, buscando entender qué causaba los diferentes sonidos.
Así, descubrió que los tonos musicales que resultaban agradables al oído estaban relacionados con proporciones matemáticas sencillas. En sus experimentos con una monocordio (un instrumento con una sola cuerda), Pitágoras estableció que:
- Cuando una cuerda se dividía en dos partes iguales (relación 1:2), se producía una octava.
- Cuando la relación entre las partes de la cuerda era de 2:3, se generaba una quinta.
- Una proporción de 3:4 producía una cuarta.
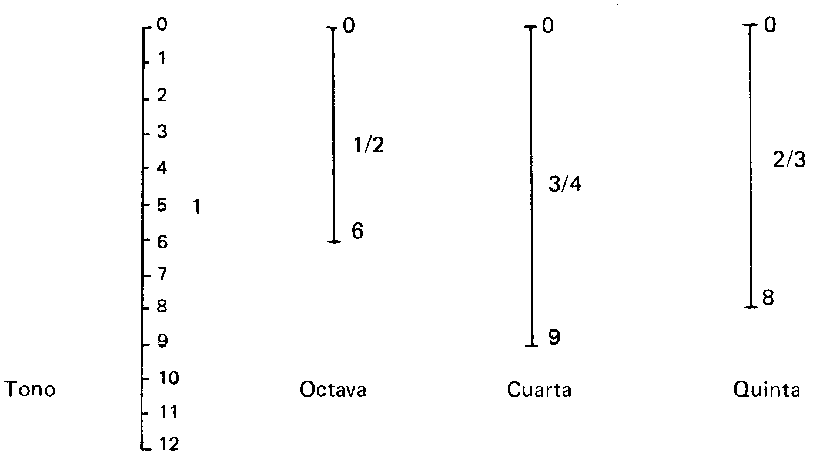
Estos descubrimientos llevaron a Pitágoras a formular la idea de que la música estaba gobernada por principios matemáticos, y que la armonía musical podía explicarse a través de relaciones numéricas.
La tetraktys y las proporciones musicales
Pitágoras introdujo la tetraktys, una figura triangular formada por diez puntos dispuestos en cuatro filas. Esta figura simboliza la perfección y contiene los primeros cuatro números: 1, 2, 3 y 4. La suma de estos números es 10, que representa la totalidad y la unidad. Las proporciones que surgen de la tetraktys también forman las relaciones armónicas en la música, mostrando la conexión entre la matemática, la música y la naturaleza.
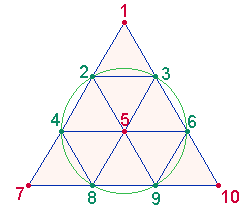
- 1:2 – Octava
- 2:3 – Quinta
- 3:4 – Cuarta
Esto consolidó la idea de que la música es una expresión directa del orden numérico en el mundo.
La Música y la Filosofía Pitagórica
Para Pitágoras, el descubrimiento de las proporciones musicales no fue solo un avance técnico, sino que tuvo profundas implicaciones filosóficas. Pitágoras y su escuela creían que los números no solo eran útiles para medir y contar, sino que representaban el principio subyacente de todas las cosas en el universo.
Armonía y orden cósmico
Pitágoras entendía que, al igual que en la música, el universo estaba regido por proporciones y armonías matemáticas. Esta idea dio lugar a su famoso concepto de la música de las esferas, la creencia de que los planetas y las estrellas, al moverse en sus órbitas, producían una especie de música cósmica inaudible para los seres humanos. Este orden cósmico no era solo estético, sino que reflejaba una verdad profunda: el universo estaba estructurado de manera matemática y armoniosa, y comprender estas proporciones significaba acercarse a la comprensión de la realidad misma.
El alma y la música
Otro aspecto central de la filosofía pitagórica es la relación entre el alma y la música. Pitágoras creía que la música podía influir en el alma, armonizándola y purificándola. Al igual que los intervalos musicales seguían proporciones numéricas precisas, el alma humana también podía alcanzar un estado de armonía cuando se ajustaba a los principios universales. La música, por lo tanto, no era solo un arte o entretenimiento, sino una herramienta para la purificación espiritual.
La Matemática y la Música: Un Lenguaje Universal
El descubrimiento de Pitágoras de que la música seguía proporciones matemáticas llevó a un enfoque filosófico más amplio: el mundo físico y el mundo de los números estaban conectados de manera intrínseca. Pitágoras y sus seguidores creían que los números eran el principio que estructura toda la realidad, y que, a través del estudio de las matemáticas, uno podía desvelar los secretos del cosmos.
Proporciones y armonía en la naturaleza
Este enfoque matemático no se limitó solo a la música. Pitágoras también observó que las proporciones que rigen la música se reflejaban en otras áreas de la naturaleza y el arte. Por ejemplo, el uso de la sección áurea, una proporción matemática que aparece en la naturaleza (en conchas marinas, flores, e incluso galaxias espirales), fue visto por los pitagóricos como una manifestación de las mismas leyes universales que gobernaban la música.
El papel de la matemática en el conocimiento
Para los pitagóricos, las matemáticas no solo servían para describir el mundo, sino que eran la clave para comprender la realidad en su totalidad. Los números eran vistos como entidades divinas, y el estudio de las matemáticas era una especie de disciplina espiritual. El descubrimiento de las proporciones musicales reforzó la idea de que el orden y la belleza del cosmos podían expresarse en términos numéricos, y que, a través del estudio de las matemáticas, los seres humanos podían participar en ese orden divino.
La Música y la Geometría: La Conexión con la Geometría Sagrada
El enfoque pitagórico también estableció una profunda conexión entre la música y la geometría. Si bien la geometría ya se estudiaba en Grecia antes de Pitágoras, fue su escuela la que empezó a ver la geometría como un reflejo de los mismos principios que rigen la música y el cosmos.
Figuras geométricas y proporciones
Pitágoras y sus seguidores estudiaron diversas figuras geométricas y observaron que, al igual que la música, estas formas estaban regidas por proporciones matemáticas. El pentagrama, una figura central en el simbolismo pitagórico, tenía proporciones que se correspondían con la sección áurea, una proporción que también se encuentra en los intervalos musicales. Estas relaciones geométricas eran vistas como manifestaciones visuales de la armonía universal que Pitágoras había descubierto en la música.
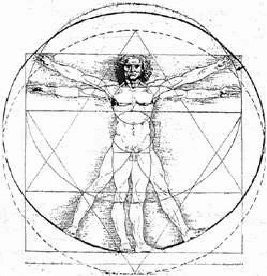
Geometría sagrada y armonía cósmica
La conexión entre la música y la geometría también influyó en lo que más tarde se llamaría geometría sagrada, la idea de que ciertas formas y proporciones geométricas tienen un significado profundo y espiritual. En la geometría sagrada, formas como el círculo, el triángulo y el pentágono son vistas como representaciones simbólicas de las leyes que rigen el cosmos, las mismas leyes que Pitágoras descubrió en la música.
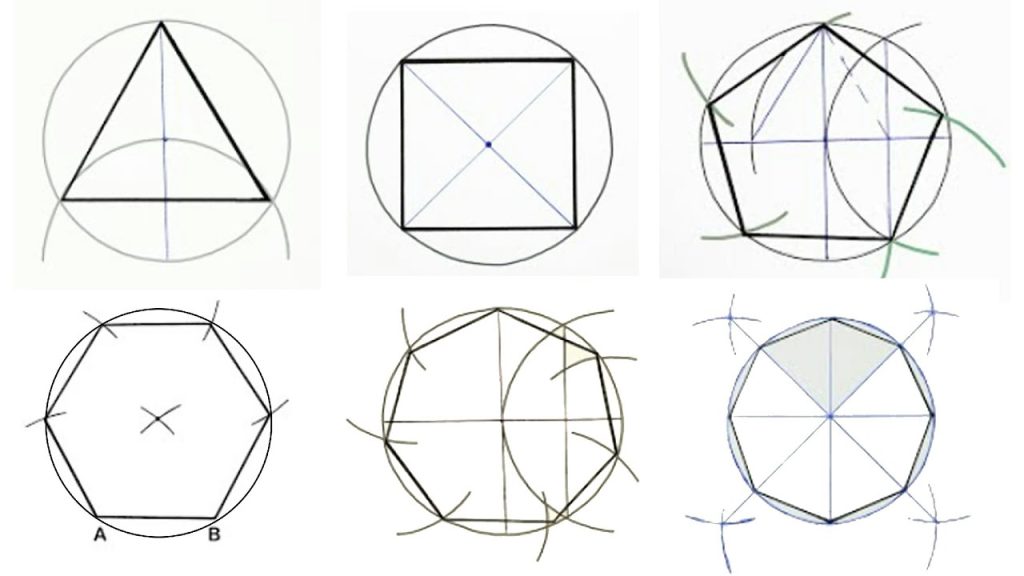
El descubrimiento de Pitágoras de las proporciones matemáticas que rigen la música no solo lo estableció como el «inventor» de la música como ciencia, sino que también tuvo profundas derivaciones filosóficas, matemáticas y geométricas. Para Pitágoras y su escuela, la música era una manifestación audible de los principios universales que rigen el cosmos. A través del estudio de las proporciones musicales y las matemáticas, los seres humanos podían comprender mejor el orden del universo y, al hacerlo, participar en su armonía divina. Esta conexión entre música, matemáticas y geometría sigue siendo una de las contribuciones más duraderas de Pitágoras al pensamiento occidental.
Video recomendado: